Post

---

The More You Know, the More You Don’t Know

I was fiddling around with complex numbers and suddenly, something horrible happened. Everything I thought I knew crumbled before me and I had a palpable taste of defeat in my mouth. Curse you, complex numbers.

I was fiddling with the expression:

$$ f(x) = x^{i \pi} $$ where $i=\sqrt{-1}$, just to see how the argument changed with $x$ for my intuition, but something much worse happened.

Plugging in a negative $x$ made $|f| \approx 0.00005172318$. “Nonsense!” you cry from behind your screen, “a number raised to an imaginary exponent lies on the unit circle!”, you protest. “The author is clearly writing pulp!” you holler… well I cannot deny that.

But lo and behold, my computer verifies that it actually does so. When plotted for varying $x$, the unit circle we know and love instantaneously shrinks to make a teeny circle for negative $x$.

Why? What sort of mathematical jackassery is going on in complex land that’s causing this?

Plotting for Intuition

A great technique to have up your sleeve is how to visualise an interesting result.

Plotting argument and magnitude in this case (since we are playing in the complex plane) is a very convenient method to build intuition.

If we plot $f(x)$ for $x \in [-1,1]$ the following result is gained (after ‘unwrapping’ the argument);

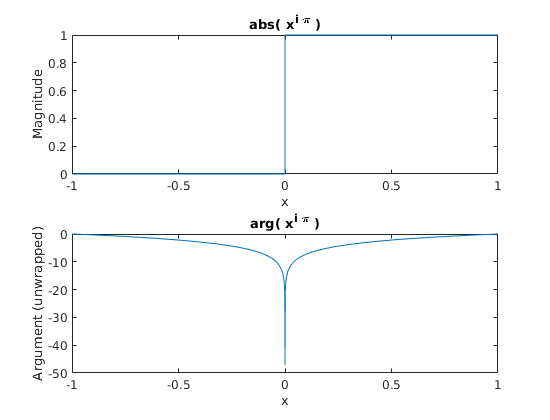
Interesting. What if we try a new function, $g(x) = x^{-i \pi}$? Of course, when $x$ is positive, the magnitude will also be one, and at the point that $x=e$ ($e$ being Euler’s constant) $f(e) = g(e) = e^{i \pi} = e^{-i \pi} = -1$. Alright! Let’s plot that too for the range we have and see what’s going on.

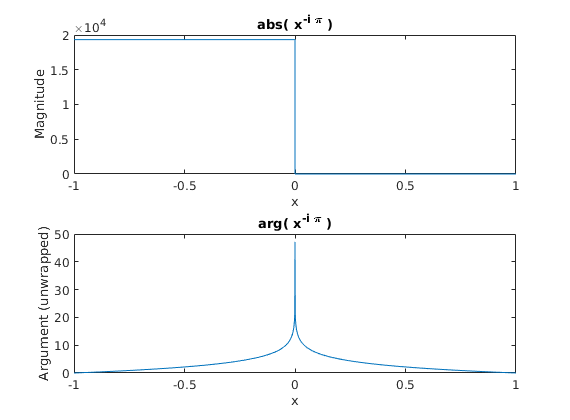
Although you’re tempted to scream “what the f”, the $\approx 10^4$ magnitude when x is negative is somewhat expected here, as $g(x) = \frac{1}{f(x)}$.

So where do we go from here? Well, the argument on the plot for $f(x)$ looks suspiciously like a logarithm, maybe this is hinting at rearranging the equation for $f$.

We can rearrange as follows:

$$ x^{i \pi} = e^{\ln (x^{i \pi}) } = e^{i \pi \ln {x}} $$ Gosh darn that’s a logarithm in there. But we are dealing with a negative $x$, and logarithms are only defined for positive $x$, right?

Logarithms, when you’re going through hell, keep going

Much to my disbelief, a logarithm of a negative number is possible, albeit with a bit of groping around with algebra and Euler’s identity.

$$e^{i \pi} + 1 = 0$$ $$e^{i \pi} = - 1 $$ $${i \pi} = \ln (- 1) $$

Now using the log identities we know and love,

$$\ln (-1) + \ln(|x|) = \ln(-|x|)$$

And substituting for $\ln (-1)$,

$$ \ln(- |x|) = \ln(|x|) + i \pi$$

Hooray hoorah hooray! We’ve cracked the logarithm of a negative number. This is more intuitive if we use a complex number, $z$ to run this course and do the derivation again for complex numbers.

$$ \text{Let} \quad z = r e^{i \arg(z)}$$ $$\ln (z) = \ln ( r ) + i \arg(z) $$

And given that for the case of a negative number $x$, the argument is simply $ \pi$.

Now recycling our freshly “discovered” negative-logarithm for the general case of a complex number $z$:

$$f (z) = e^{i \pi (\ln (z)) } \qquad x \in \mathbb{C},; z \neq 0 $$ $$f (z) = e^{i \pi (\ln (|z|) + i \arg(z)) } \qquad z \in \mathbb{C},; z \neq 0$$ $$f (z) = e^{i \pi (\ln (|z|))} e^{-\pi\arg(z) } \qquad z \in \mathbb{C} ; z \neq 0 $$

Now, we finally let $x$ be a negative real number, $\arg(x) = \pi$. $$f (x) = e^{i \pi (\ln (|x|))} e^{-\pi^2 } \qquad x \in \mathbb{R},; x<0 $$ Since $|e^{i \pi (\ln (|x|))}| = 1$, we can now comfortably say $|f(x)| = e^{-\pi^2}$ if $x<0$, or more generally for any $x \in \mathbb{R}$:

$$ |x^{i \pi}| = \begin{cases} e^{-\pi^2} & x<0 \ \text{undefined} & x=0 \ 1 & x>0 \ \end{cases} $$

And slowly the headache subsides, as we finally try and place $e^{-\pi^2}$ into our calculator to get: $$e^{-\pi^2} \approx 0.00005172318$$

Important Lessons and My Own Constant

Something you can really learn from this is that it’s not wise to make blind assumptions for things all the time, because more often that not things are more complicated than they appear. I am not disputing that it’s nice to have a gut feel for something, but for a lot of things in life you shouldn’t judge a book by its cover (to be cliché).

Another learning point is to just try things out! See something mathematically strange happening? Don’t immediately assume you’re wrong, play with the discovery, develop an intuition and you’ll learn something along the way and grow as a person.

Now that I’ve been upbeat and nice, I feel like I can wrap up this post by doing something for myself now. Since nobody has claimed a name for $e^{-\pi^2}$ (after a fair amount of searching) I henceforth narcissistically name it “William’s Constant”, as of May 25th 2019.